DK's R self study: Normal distribution

When it comes to the probability distribution, you might be think two distributions.

Discrete distribution
Continuous distribution

Normal distribution is very popular distribution which is a continuous probability distribution defined by below formula.

$f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{ -\frac{(x-\mu)^2}{2\sigma^2} }$

A normal distribution has some features.

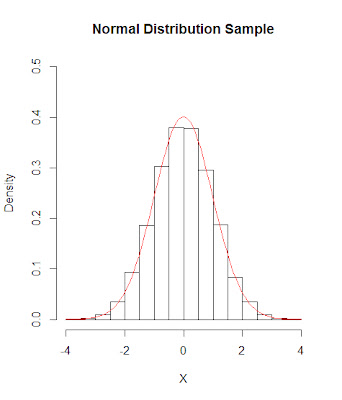
Normal distribution is symmetric with respect to mean value. (upper graph mean =0)
Probability is measured over intervals, not single point (Calculated by integral) $\Pr[a\le X\le b] = \int_a^b f(x) \, dx$
Total integral of the probability is 1 $\operatorname{E}[X] = \int_{-\infty}^\infty x\,f(x)\,dx.$ = 1
Good normal distribution is proportion to sample size. (check out the kurtosis,skewness)

As I mentions, normal distribution is continuous density distribution,

we need a special table to calculate the probabilithy or x-axes variable, we called this

"Z score table" check out the z score through your internet.

Fortunately, R provides a useful function to calculate z score such as

pnorm(x, mean, sd) => gives the probability of getting a value from the cumulative probability function

qnorm(p, mean, sd) => gives the value that is the Pth percentile from cumulative probability function.

Let's take a value from our assumption.

1) Get a probability of x-axis 2 from the normal distribution that their mean is 0 and standard deviation is 2.

2) Get a probability of x-axis 4 from the normal distribution that their mean is 0 and standard deviation is 2.

3) Get a x-axis value that is the 0.8413447% from the normal distribution that their mean is 0 and standard deviation is 2.

4) Get a x-axis value that is the 0.9772499% from the normal distribution that their mean is 0 and standard deviation is 2.

> pnorm(2, 0 ,2)

[1] 0.8413447

> pnorm(4, 0 ,2)

[1] 0.9772499

> qnorm(0.8413447, 0,2)

[1] 2

> qnorm(0.9772499, 0,2)

[1] 4.000001

Are you aware that upper 2 questions are related with bottom 2 question ?

DK's R self study

2013년 2월 14일 목요일

Normal distribution - No16

댓글 없음:

댓글 쓰기